This hash function is not based on large prime numbers, like those based on RSA.
This hash function is based on the Weierstrass function.
The Weierstrass function was invented by the German mathematician Karl Weierstrass (1815-1897), It is written Karl Weierstraß, but it is said Weierstrass to adapt it to the language.
The Weierstrass function has fractal behavior.
The Weierstrass function has the property that its graph repeats at different scales. This means that if you take two very close real numbers, the pattern of the Weierstrass function’s graph repeats on a smaller scale.
the preimage of any point is countably infinite of no-countably infinite sets, that is: א*c
Some graphs of the Weierstrass function:
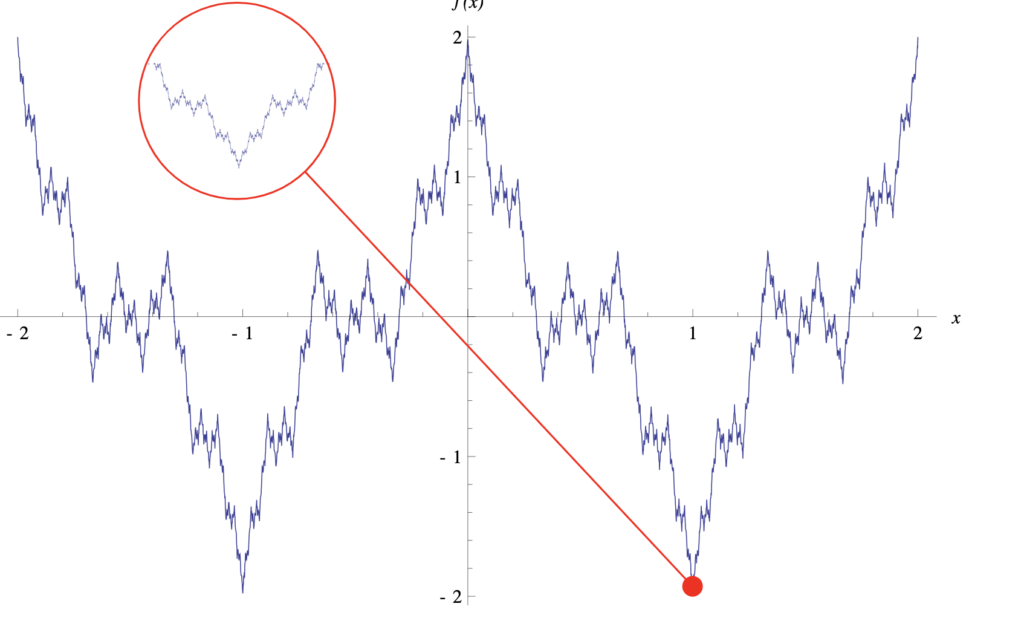
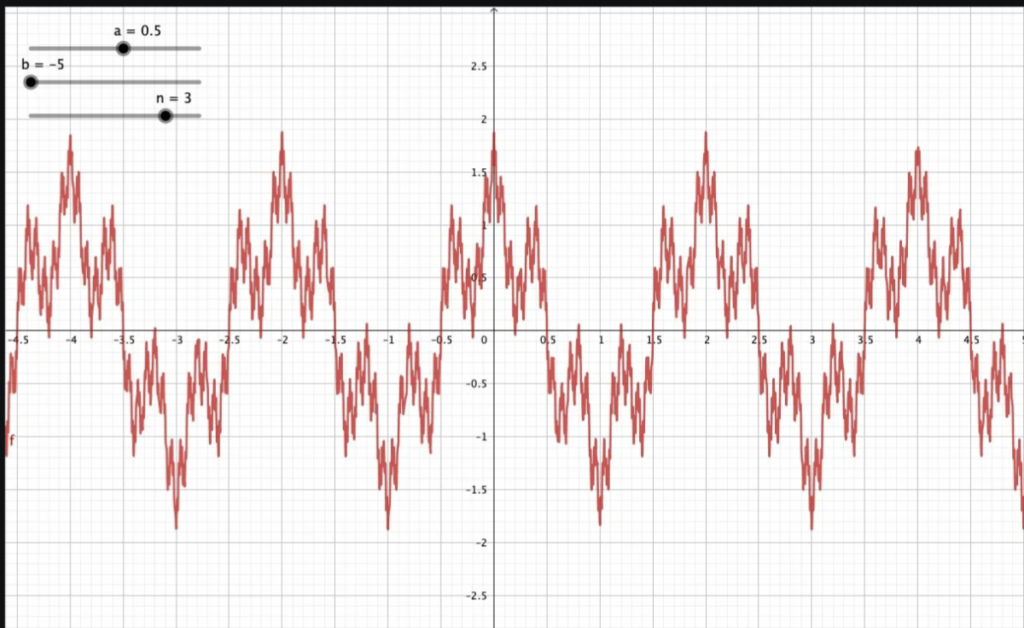
Small changes in the input value can produce significant changes in the output value. This is known as sensitivity to initial conditions.
The Weierstrass function has a property called “deterministic chaos“, which means that small variations in the input value can produce very different, seemingly random results.
I believe that RSA-based algorithms are easy to understand but difficult to break, due to the computational power of calculation.
In a few years I think that computing power will grow a lot and we will be able to break the RSA.
A Weierstrass-based function will not be broken by computational power, but by number theory.
If someone can break it, they would not only be breaking my hash function, but also solving a mathematical problem.
There are many chaotic functions, I chose Weierstrass because it is very well studied.
The Weierstrass function has no global maximum or minimum.
This is due to the fractal and chaotic nature of the function, which makes it very sensitive to changes in the input value and causes it to produce very varied and seemingly random outputs.
The Weierstrass function is
f(x) = ∑[a^n * cos(b^n * π * x)]
The sum is obviously from 0 to infinity, infinite terms.
In the Weierstrass function, the product of a and b is required to satisfy a specific condition:
a * b > 1 + 3π/2
If a * b does not satisfy this condition, the series may not converge.
- a: is a real constant, with 0 < a < 1.
- b: is a positive odd integer.
- x: is the independent variable, which can be any real number.
- n: is a natural, the index of the summation, the index of each term
how to implement conditions in java:
- double a: 0 < a && a < 1
- int b: b > 0 && (b % 2 == 1)
- int n: n > 0
- (a*b) > (1 + (3*Math.PI/2))
instead of double working with BigDecimal, I had to change it, since I manipulate numbers with more than 70 digits and I lose precision.
approximately:
1 + 3π/2 ≈ 5.71238898038469
The hash function can take as parameter x as a number with 40 integer digits and 30 decimal digits, for example.
In my case, I don’t know how to add infinite terms, I will only add 70,000 terms, that is, 70,000 iterations.
I will then upload a Java hash function library to Maven Central.
For precision in digits you should not use double, you should use Taylor series to perform operations with cosines (do not use ready-made ones) for example, we are talking about a precision of 100 decimal places.