links:
An AVL tree (Adelson-Velskii and Landis), two people, the initials of AVL come from their surnames.
Website to create an animated AVL: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
Is a type of self-balancing binary search tree (BST self balancing). It was invented in 1962 by Soviet computer scientists Adelson-Velskii and Landis.
The height of an AVL tree is always O(log(n)), where n is the number of nodes in the tree.
The idea is to take advantage of the fact that the height is proportional to log(n) and that it is a binary search tree (if both things are true it is an AVL) and we must always maintain that it is AVL, therefore its operations have a cost O(log(n))
An AVL tree is a special type of BST where the height of the left and right subtrees of any node never differ by more than 1. If this rule is broken, the tree is considered unbalanced, and a rotation must be applied.
In the AVL, each node has a balance factor (BF).
The BF must be kept up to date on each node.
To maintain balance its value at each node can be 0,-1,+1.
If the BF is a value other than -1,0,+1, if it is different in a node, it is said that the tree is unbalanced.
balance factor = right subtree height - left subtree heightIf a node is unbalanced, the tree must be balanced by rotating it and adjusting its value location.
if n is a node, it is called left heavy if BF(n) < 0
If n is a node, it is called right heavy if BF(n) >0
If n is a node, it is called balanced if BF(n) = 0
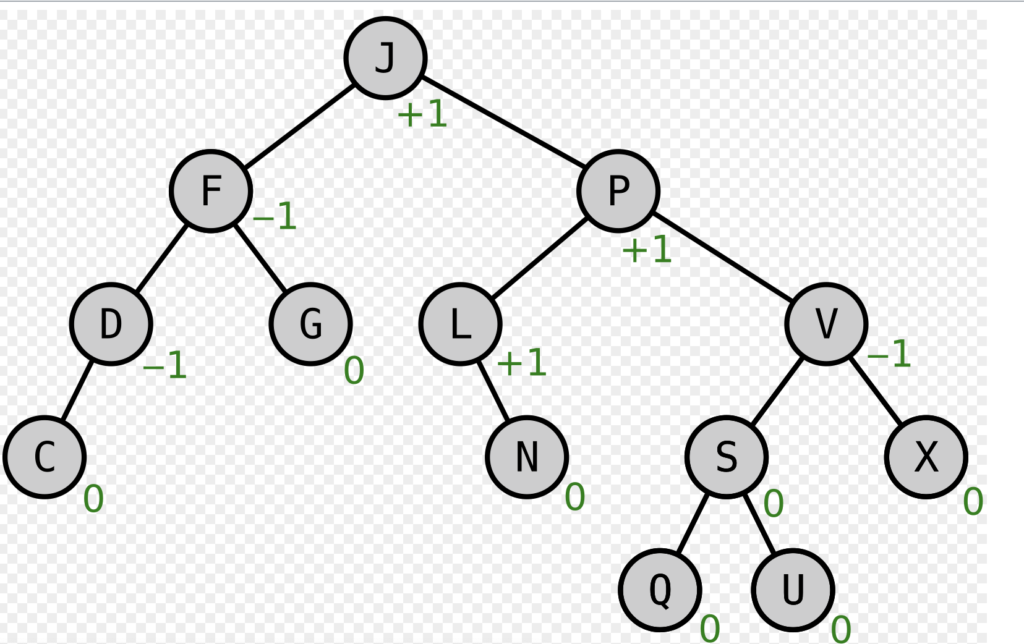
The main purpose of an AVL tree is to maintain a balance between the height of the tree and the number of nodes, allowing search, insertion, and deletion operations to be performed efficiently.
The main goal of rotations is to maintain the tree’s efficiency. If a BST becomes too unbalanced (degenerating into a linked list), search, insert, and delete operations can degrade to O(n) time complexity.
By ensuring that the height remains logarithmic with rotations, AVL trees ensure that these operations maintain an optimal complexity of O(logn).
Types of imbalances
There are four types of imbalances in an AVL tree:
- Left-left imbalance (LL): The unbalanced node has a left child and the left child also has a left child.
- Left-right imbalance (LR): The unbalanced node has a left child and the left child has a right child.
- Right-right imbalance (RR): The unbalanced node has a right child and the right child also has a right child.
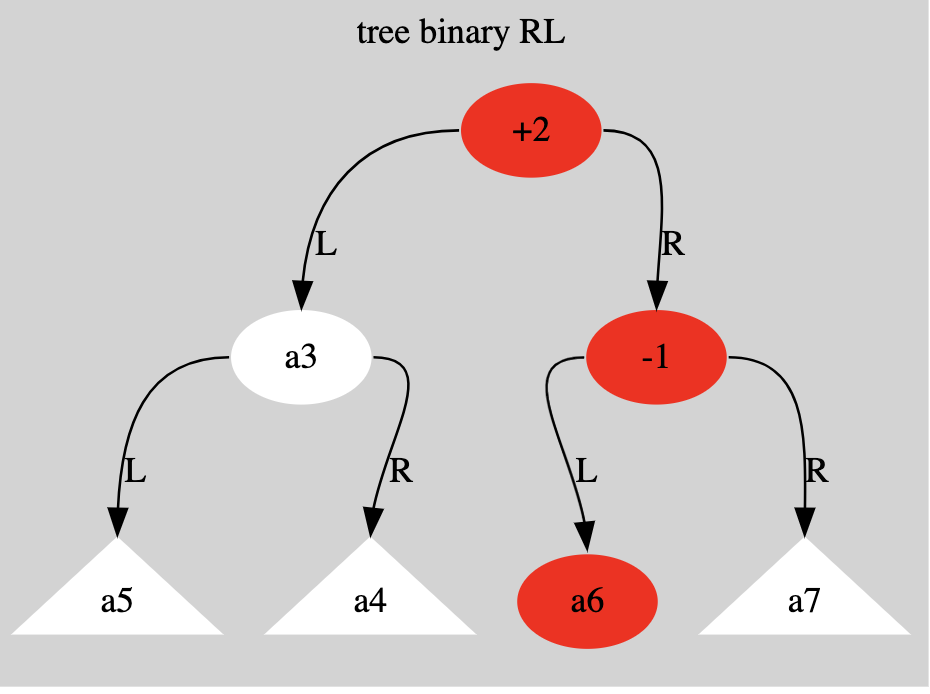
- Right-left imbalance (RL): The unbalanced node has a right child and the right child has a left child.
There are four basic types of rotations, which are grouped into two categories: simple (a single rotation) and double (two consecutive simple rotations).
Rotations
- RRot (right rotation): right rotation
- LRot (left rotation): left rotation
For each type of imbalance, a specific rotation must be performed:
- LL imbalance: Right rotation (RRot) at node. simple balancing.
- LR imbalance: Left rotation (LRot) at node->left followed by a right rotation (RRot) at node. double balance
- RR imbalance: Left rotation (LRot) at node. simple balancing.
- RL imbalance: Right rotation (RRot) at node->right followed by a left rotation (LRot) at node. double balance.
If the highlight looks wrong, it’s a WordPress error.
Examples of types of imbalance in drawings.
The triangles represent tree structures and the round ones are nodes.
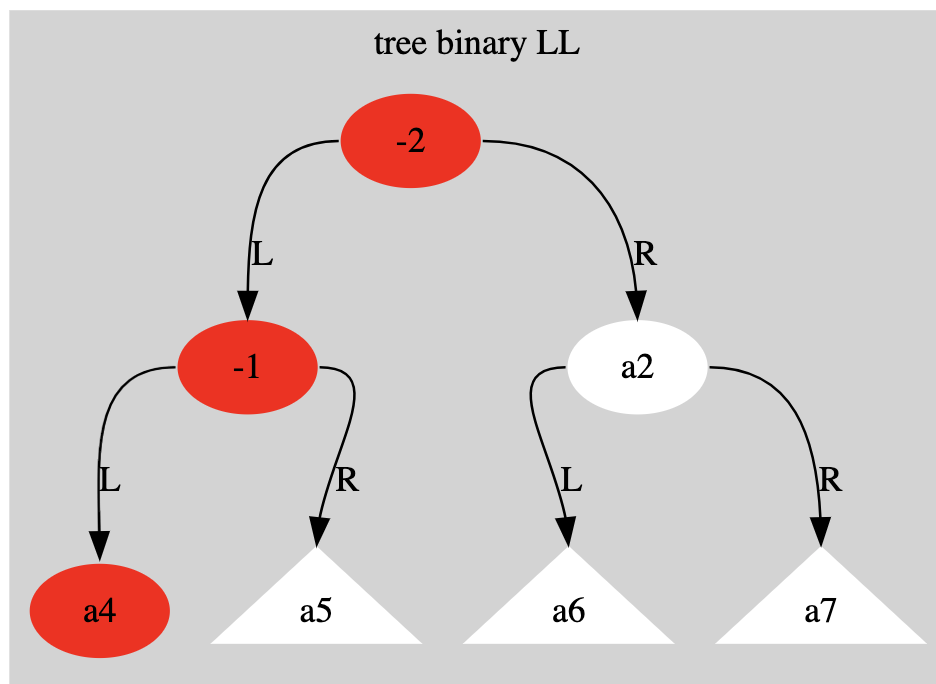
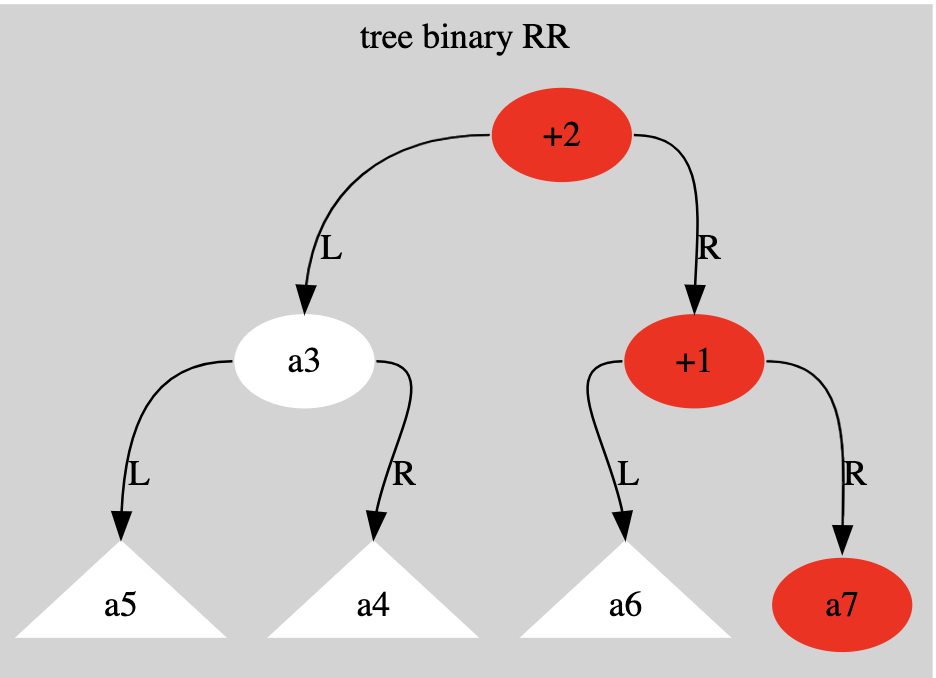
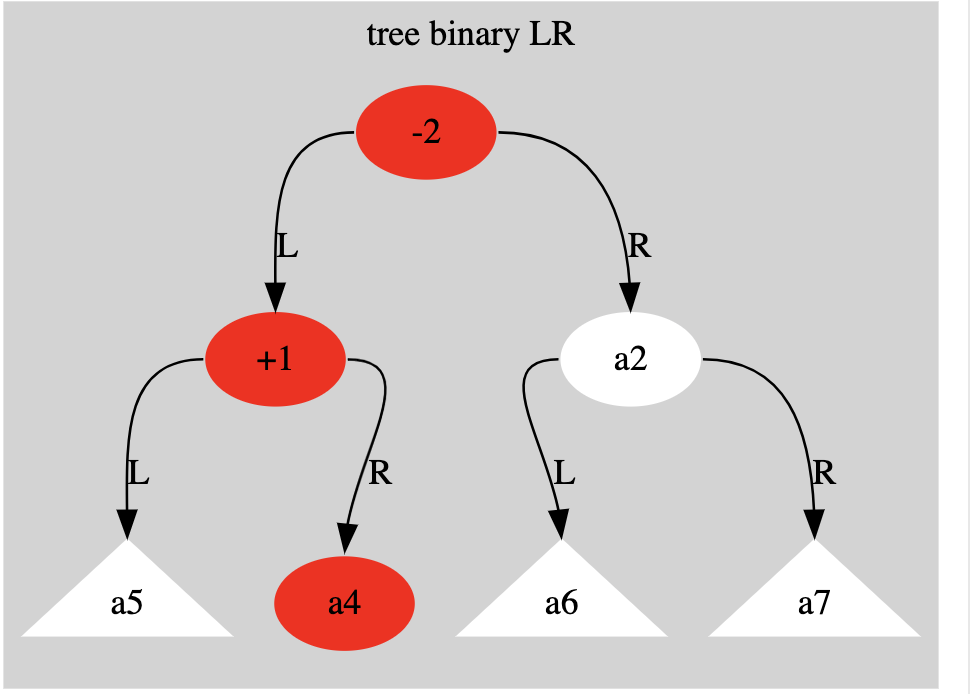
example of an imbalance:
and how to balance it
how is it balanced:
Left rotation algorithm in java
public Node leftRotation(Node node) {
if (node == null) {
return null;
}
Node temporary = node.right;
node.right = temporary.left;
temporary.left = node;
node.height = 1 + Math.max(height(node.left), height(node.right));
temporary.height = 1 + Math.max(height(temporary.left), height(temporary.right));
return temporary;
}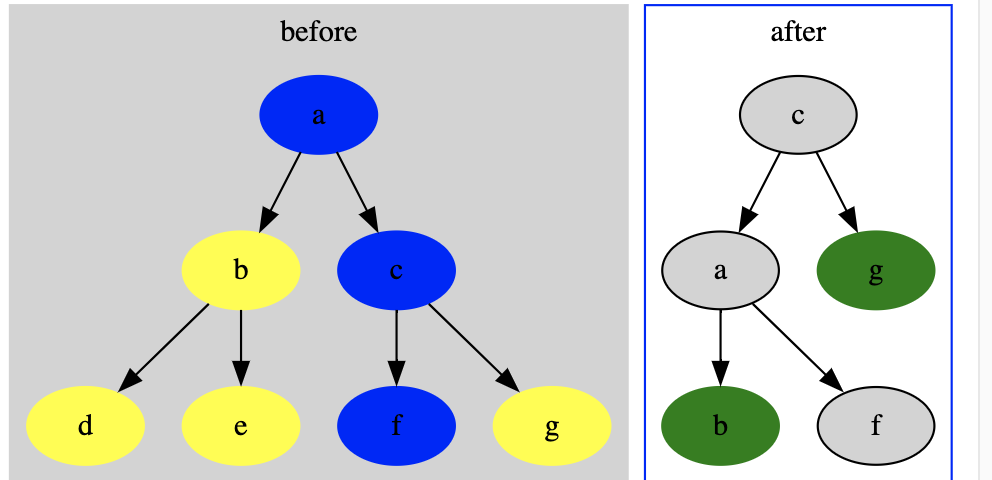
an example of left rotation entering node “a” as a parameter.
- What is in yellow is not moved, remains pointing from the same place.
- The blue will be moved, “c” on its left points to “a”, on its right it does not change.
- The green remains pointing from the same place.
- We changed the header of “a” to “c”.
- It’s like pointing to “c” with an invisible arrow and pulling it, only changes the pointer to “f”.
- We only need to update the heights of “a” and “c”, not “f”, the rest have their correct height.
Right rotation algorithm in java
public Node rightRotation(Node node) {
if (node == null) {
return null;
}
Node temporary = node.right;
node.left = temporary.right;
temporary.right = node;
node.height = 1 + Math.max(height(node.left), height(node.right));
temporary.height = 1 + Math.max(height(temporary.left),
height(temporary.right));
return temporary;
}
Height of a Node
public int height(Node<T> node) {
if (node == null) {
return 0;
} else {
return 1 + Math.max(height(node.getLeftNode()), height(node.getRightNode()));
}
}Balance factor (FE)
public void updateBalanceFactor() {
int leftHeight = height(this.leftNode);
int rightHeight = height(this.rightNode);
this.balanceFactor = rightHeight - leftHeight;
}
Here is how an AVL tree works:
Properties of AVL tree
- It is a binary search tree, that is, for each node, all elements in the left subtree are less than the node, and all elements in the right subtree are greater than the node.
- The height of the left and right subtrees of each node differs by at most 1.
Operations on an AVL tree
- Search: An element is searched for in the tree in a similar way to a binary search tree.
- Insertion: A new element is inserted into the tree. If the insertion causes an imbalance in the tree, rotations are performed to restore the balance.
- Deletion: An element is removed from the tree. If the deletion causes an imbalance in the tree, rotations are performed to restore the balance.
Rotations on an AVL tree
To maintain the balance of the tree, rotations are performed when an element is inserted or deleted.
There are four types of rotations:
- Left rotation: The tree is rotated to the left when the right subtree of a node is too tall.
- Right rotation: The tree is rotated to the right when the left subtree of a node is too tall.
- Left-right rotation: The tree is rotated left and then right when the right subtree of a node is too tall and the left subtree of the right node is too tall.
- Right-left rotation: The tree is rotated right and then left when the left subtree of a node is too tall and the right subtree of the left node is too tall.
Advantages and disadvantages of AVL trees
Advantages:
- Efficient search: AVL trees allow efficient searches, with a time complexity of O(log n).
- Efficient insertion and deletion: AVL trees allow efficient insertions and deletions, with a time complexity of O(log n).
Disadvantages:
- Additional complexity: AVL trees require additional complexity to keep the tree balanced, which can increase the execution time in some cases.
- Additional memory requirements: AVL trees require additional memory to store the height of each node and perform the necessary rotations.
The binary trees were graphed with “Graphviz Online”: https://dreampuf.github.io/GraphvizOnline/
Example of how to draw the LL binary tree
digraph G {
subgraph cluster_0 {
style=filled;
color=lightgrey;
node [style=filled,color=white];
a5 [shape=triangle];
a6 [shape=triangle];
a7 [shape=triangle];
a0 [color=red,label="-2"];
a3 [color=red,label="+1"];
a4 [color=red];
a0 -> a3 [label="L",tailport=w, headport=n];
a0 -> a2 [label="R",tailport=e, headport=n];
a3 -> a4 [label="L",tailport=w, headport=n];
a3 -> a5 [label="R",tailport=e, headport=n];
a2 -> a6 [label="L",tailport=w, headport=n];
a2 -> a7 [label="R",tailport=e, headport=n];
label = "tree binary LL";
}
}again, so that you understand
This is for me, so I understand clearly
- T1 is the left subtree of A (there may be multiple nodes or none)
- T2 is the subtree of B and will be moved
- T3 in simple rotations is usually node C
- for double rotations, T3 and T4 if they are usually different nodes
- In this case you only modify nodes A, B and T2
Right-Right (RR) imbalance pattern
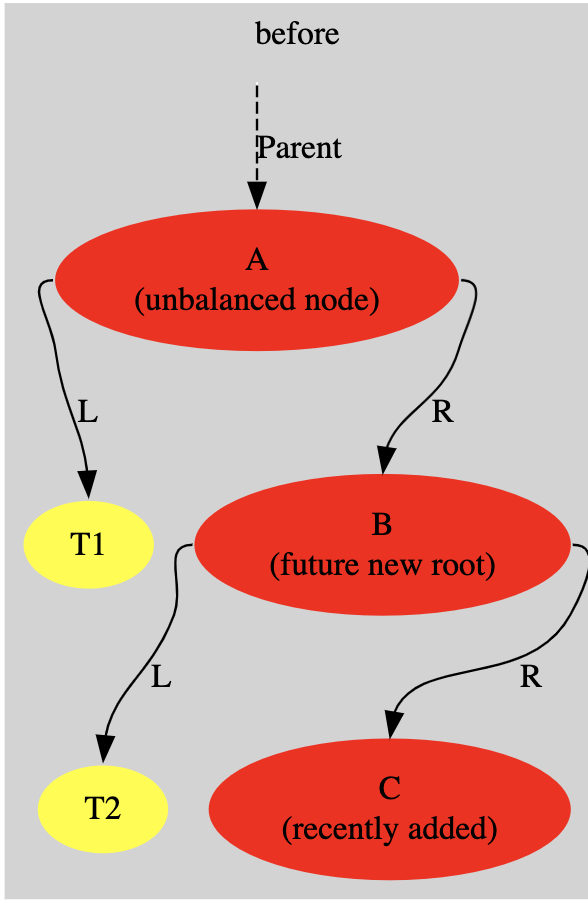
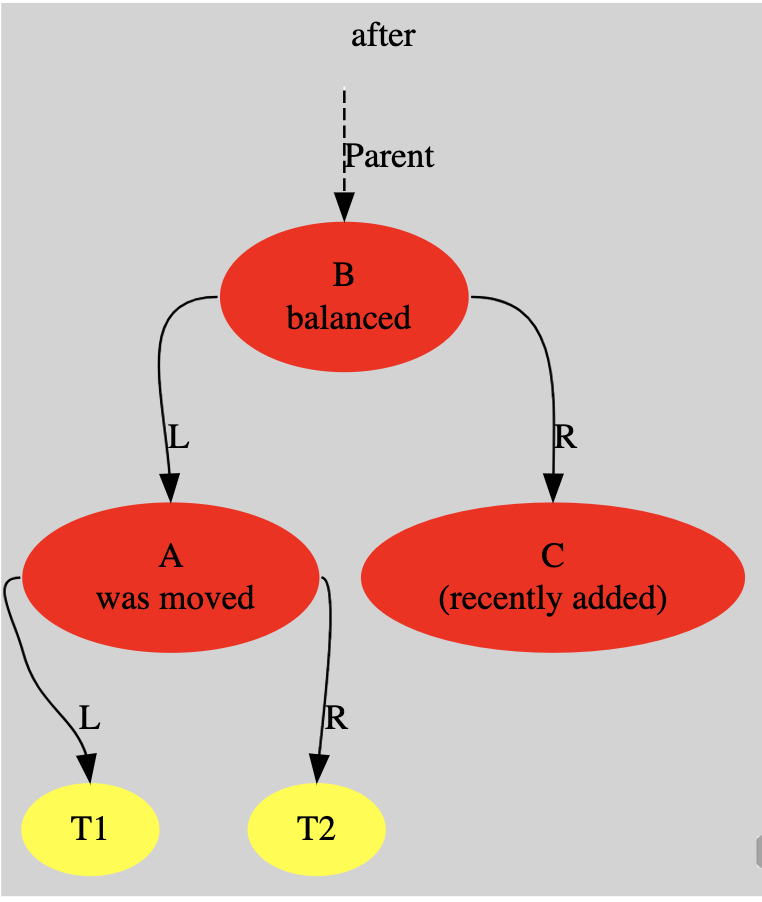
After: Displays the rebalanced tree with node B promoted as the new root of the subtree, and subtree T2 has been successfully reassigned to the right child of node A
Why is it called simple rotation to the left and RR (right right)?
- The reason why RR (Right-Right) imbalance correction is called Simple Left Rotation has to do with the physical direction of rotation that is performed on the shaft.
- The name RR (Right-Right) describes the pattern of imbalance that is detected in the tree
- The name “Left Rotation” describes the action taken to correct this imbalance, which is the physical movement of the structure
- This twist “lifts” the central node B and makes it the new root of the substructure, causing the old parent A to fall to the left side
- RR names the problem, and Rotation Left names the solution (the action of turning)
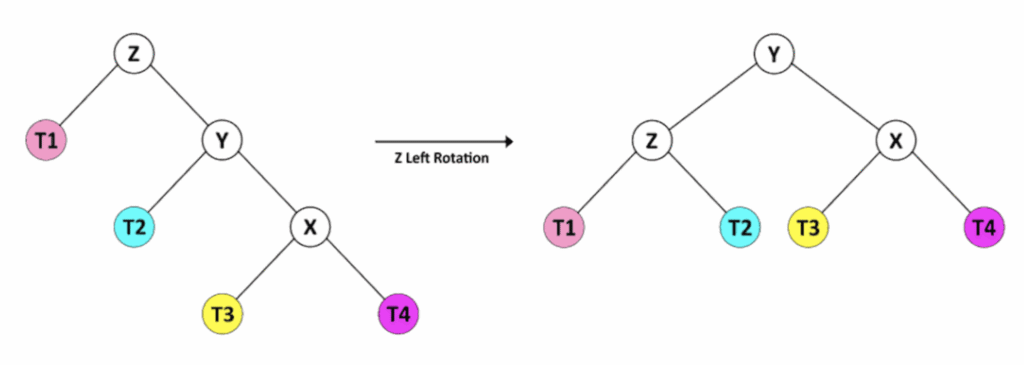
A simple rotation to the right is analogous
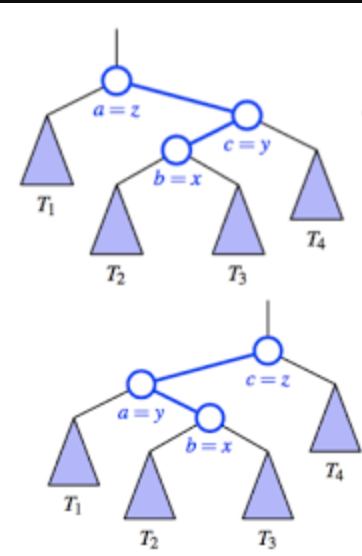
A Right-Left (RL) rotation is a double rotation used to rebalance a tree
This process involves a right rotation at the child node, followed by a left rotation at the parent node
A right-to-left rotation is necessary when a node’s balance factor becomes (-2), indicating that its right subtree is two levels deeper than its left subtree. The DI case is specifically identified by this imbalance and because the right child’s balance factor is (+1)
before:

after:

a double LR rotation is analogous